Das Pohl'sche Pendel mit Unwucht

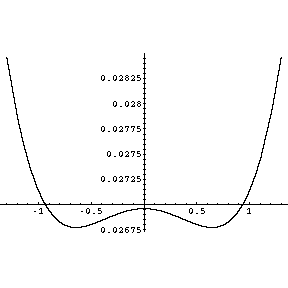
Das Pohl'sche Drehpendel besteht aus einer drehbar gelagerten Scheibe, die durch eine Spiralfeder (Uhrfeder) mit einem Rahmen verbunden ist und Drehschwingungen ausführen kann. Diese sind in guter Näherung harmonisch. Um eine anharmonische Schwingung zu erhalten, wird eine Unwucht an der Scheibe befestigt, die ihren höchsten Punkt in der Ruhelage des Pendels erreicht. Dem parabelförmigen Potential wird also eine Cosinusfunktion überlagert. Mit dem benutzten Versuchsaufbau bekommt der Potentialverlauf folgende Gestalt (Auslenkung im Bogenmaß, Potential in willkürlichen Einheiten):

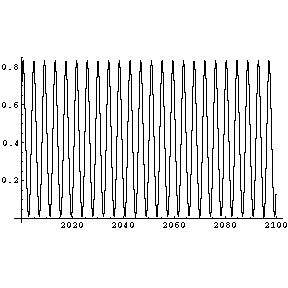
Man erkennt zwei stabile und einen instabilen Fixpunkt. In der Simulation wird nun eine harmonische Schwingung eingekoppelt und des Pendel zu einer anharmonischen Schwingung angeregt. Gezeigt ist hier für verschiedene Dämpfungen links ein Ort/Zeit-Diagramm und rechts ein Phasenraumdiagramm. Von oben nach unten wird die Dämpfung reduziert. Alle anderen Parameter sind konstant. Jedes Diagramm enthält einen Ausschnitt von 100s, dem eine Einschwingzeit von 2000s vorausgegangen ist.

Zusätzlich gibt es die Möglichkeit, die Schwingung nicht nur zu sehen, sondern auch zu hören! Dafür wurde jeweils eine Schwingung von 21600 Sekunden, also 6 Stunden simuliert und um den Faktor 1800 beschleunigt. Das Resultat ist eine 12 Sekunden lange akustische Schwingung. Diese steht nun als MP3 zum Download zur Verfügung. Der Einschwingvorgang wurde ebenfalls aufgezeichnet und ist vor allem im letzten Beipiel deutlich zu hören. Von allen Audiodateien gibt es ein Spektrogramm.

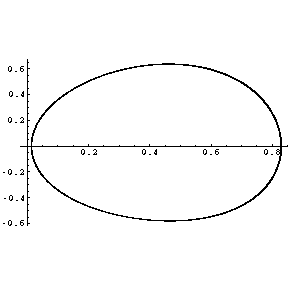		Bei hoher Dämpfung bewegt sich das Pendel nur in einem der beiden Potentialtöpfe, schwingt also um eine stabile Ruhelage. Die Bewegung ist periodisch und lässt sich als harmonische Grundschwingung mit Oberschwingungen auffassen. Diese sind im Spektrogramm gut zu erkennen.
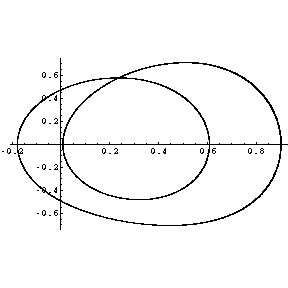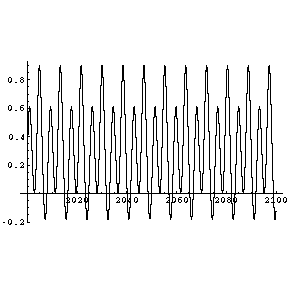
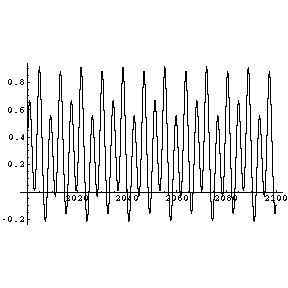
		Mit Abnahme der Dämpfung tritt hier die erste Bifurkation (Periodenverdopplung) auf. Die Bewegung ist noch periodisch, weist aber die doppelte Periodendauer auf (s. x,t-Diagramm). Im Spektrogramm erkennt man eine neue Grundfrequenz, die der Hälfte der alten Grundfrequenz entspricht.
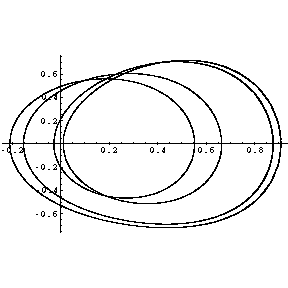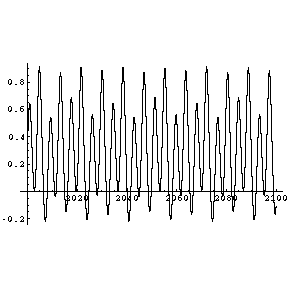
		Nach der zweiten Bifurkation ergibt sich hier die vierfache Periodendauer. Die Grundfrequenz halbiert sich erneut, im Spektrogramm treten weitere Linien auf.
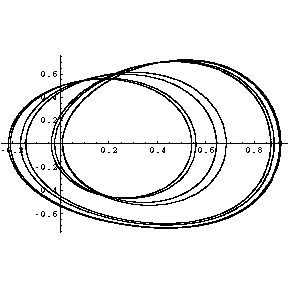		Und noch eine Bifurkation! Die Bewegung ist tatsächlich noch periodisch, mit achtfacher Periodendauer, siehe Spektrogramm.
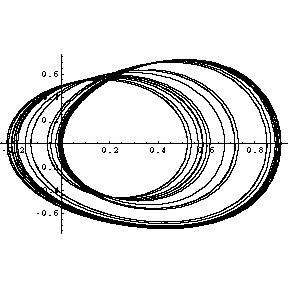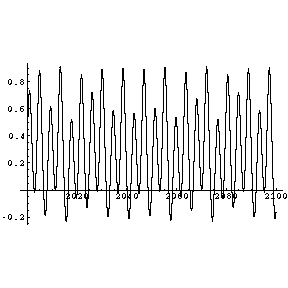
		Bei noch geringerer Dämpfung geht die Periodendauer gegen unendlich, d.h. es findet kein periodischer Vorgang mehr statt. Der Einschwingvorgang dauert unendlich lange. Hier beginnt der chaotische Bereich.
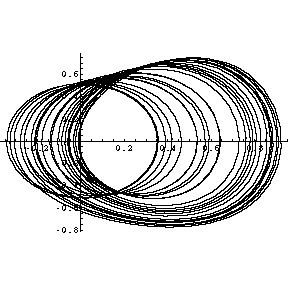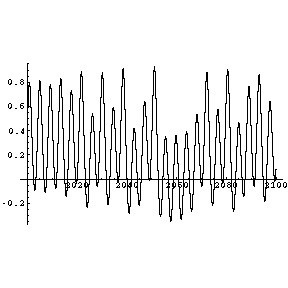
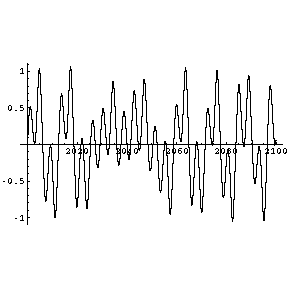
		Absolutes Chaos. Akustisch macht sich nun ein Rauschen bemerkbar.
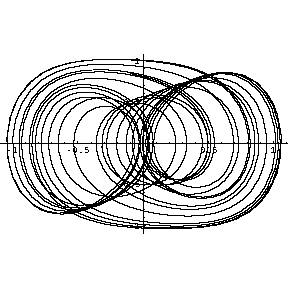		Hier bewegt sich das Pendel kurze Zeit in einem Potentialtopf und wechselt chaotisch zwischen beiden Töpfen hin und her. Das wird vor allem im x,t-Diagramm sichtbar.
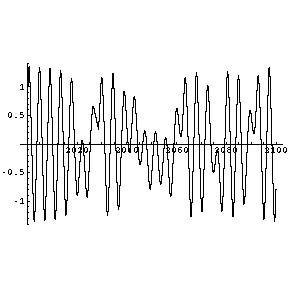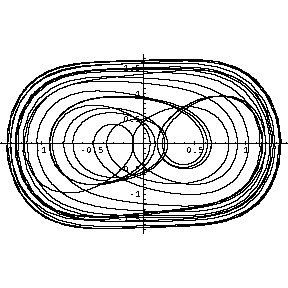		Der umgekehrte Fall tritt bei noch geringerer Dämpfung ein. Das Pendel schwingt über den Potentialberg hinweg, bleibt aber auch manchmal daran hängen und kehrt um. Das passiert wieder chaotisch. Das Rauschen ist hier besonders gut zu hören.
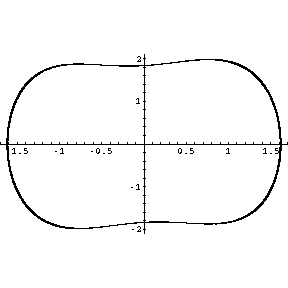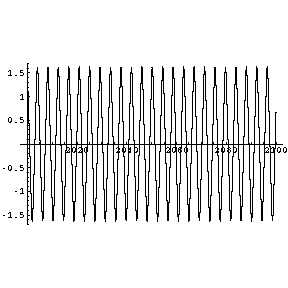
		Wenn die Dämpfung einen kritischen Wert unterschreitet, bewegt sich das Pendel wieder periodisch, diesmal aber durch den gesamten Bereich. Auf dieser Seite gibt es keine Bifurkationen. Interessant ist auch die Form des Phasenraumdiagrammes: In der Nähe des Potentialmaximums ist die Geschwindigkeit kleiner als in den Potentialminima - daher ist die Phasenraumellipse oben und unten eingedellt. Im Spektrogramm sieht man den recht langwierigen Einschwingvorgang von einigen Minuten (beschleunigt auf eine Zehntelsekunde). Dieser ist auch akustisch erkennbar.