Man betrachtet die Folge zn in der komplexen Ebene, die rekursiv definiert wird durch z0 = 0 und zn + 1 = zn2 - c. Die Menge der Punkte c, für die diese Folge nicht divergiert, bezeichnet man als Mandelbrot-Menge, benannt nach Benoit Mandelbrot. Ihre Berandung hat fraktalen Charakter und ist selbstähnlich.
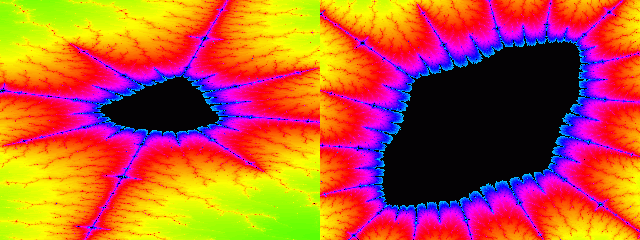
Die Mandelbrot-Menge ist in der linken Hälfte des Applets schwarz dargestellt. Die anderen Farben geben an, wie schnell die Folge für den entsprechenden Wert des Parameters c divergiert, beginnend bei Magenta für Divergenz (Überschreiten der Grenze |z| = 4) nach einem Schritt, Blau bei 256 Schritten, Cyan bei 511 Schritten, Grün bei 766 Schritten, Rot bei 1021 Schritten, Magenta bei 1276 Schritten und entsprechend zyklisch fortgesetzt. Deutlich zu erkennen ist die "Apfelmännchen"-Form, auf englisch als "apple man" bezeichnet. Es handelt sich hier also um einen "applet man".
Während links die Iterationsdauer in Abhängigkeit vom Parameter c in der komplexen Ebene aufgetragen ist, wird im rechten Fenster der Startwert z0 variiert und der Parameter c konstant gelassen. Voreingestellt ist c = 0, wodurch sich ein Kreis ergibt (der jedoch wegen der verschiedenen Maßstäbe als Ellipse erscheint). Die Berandung wird als Juliamenge bezeichnet, benannt nach Gaston Julia. Sie ist genau dann zusammenhängend, wenn der Parameter c in der Mandelbrot-Menge liegt.
Durch einen Doppelklick im linken Fenster wird der ausgewählte Parameterwert c in die Berechnung der Juliamenge übernommen. Entsprechend setzt ein Doppelklick im rechten Fenster den Startwert z0 für die Berechnung der Mandelbrot-Menge.
Das Applet verfügt über eine Koordinatenanzeige und eine Zoom-Funktion. Die Anzeige im unteren Bereich gibt die Position der Maus an. Durch Klicken und Ziehen mit der linken Maustaste lässt sich der Zoom vergrößern, mit der rechten Maustaste verkleinern.
Mit etwas Übung und der richtigen Technik (Auswählen und schrittweises Vergrößern eines entlegenen Astes der Mandelbrotmenge, setzen des Parameters für die Juliamenge durch Doppelklick in die Mandelbrotmenge und Vergrößern des Ursprungs im rechten Fenster) kann man solche Bilder erhalten:
