Liebe Freund und Verwandte,
seit meiner letzten Mail ist etwas mehr Zeit vergangen als sonst - dafür hat sich um so mehr ereignet, von dem ich nun berichten kann.
Da wären zunächst eine ganze Reihe von Vorlesungen: Wie bereits in meiner letzten Mail angekündigt höre ich zur Zeit drei "reguläre" Vorlesungen: Eine davon ist die Einführung in die Struktur der Materie. In der ersten Semesterhälfte ging es dabei in erster Linie um Festkörperphysik, wobei am Anfang auch etwas Molekülphysik behandelt wurde. Hauptschwerpunkte waren dabei Modelle von Molekülen und Festkörpern, die eine Berechnung von deren makroskopischen Eigenschaften erlauben. Beispiele solcher Eigenschaften sind Wärmekapazität (wie lange ist die Herdplatte noch heiss), Wärmeleitfähigkeit (warum fühlt sich Stahl kälter an als Holz) und Schallgeschwindigkeit (warum hört man den Zug, wenn man ein Ohr auf die Schiene legt). Als letztes und spannendstes Thema wurde die Supraleitung behandelt: In einem Supraleiter können Ströme ohne Verluste (ohne elektrischen Widerstand) fließen. Erzeugt man einen Ringstrom in einer supraleitenden Spule, so fließt dieser unbegrenzt weiter. Man benutzt dieses Verfahren um sehr hohe Magnetfelder zu erzeugen. Einziger Nachteil: Supraleitung funktioniert nur unterhalb der Sprungtemperatur. Zwar kennt man heute keramische Materialien, die "nur" mit flüssigem Stickstoff von -196°C gekühlt werden müssen (ein tolles Zeug - wer mal damit experimentiert hat, weiß, was ich meine), aber aus denen kann man keine Spulen wickeln. Die "brauchbaren" Materialien erfordern aber eine Heliumkühlung von -269°C, und die ist um einen Faktor 30 teurer.
Soviel zur angewandten Physik. Jetzt ein Sprung: Mathematik 4. Wichtigstes Thema ist die Funktionentheorie, also die Theorie differenzierbarer komplexwertiger Funktionen einer komplexen Variablen. Das klingt zunächst sehr abstrakt, aber erst bei genauem Hinsehen merkt man, dass es noch viel abstrakter ist. Deshalb summiere ich nur kurz die Ergebnisse: Mit den Hilfsmitteln der Funktionentheorie kann man bestimmte Integrale, wie sie z.B. bei der Fouriertransformation (also der Frequenzanalyse) auftreten, vergleichsweise einfach ausrechnen. Auch eine ganze Reihe von Geichungen lassen sich leichter lösen. Insbesondere Differentialgleichungen, die in der Physik sehr häufig auftreten, werden im komplexen viel einfacher.
Wo braucht man das? In der theoretischen Physik zum Beispiel. Da steht im vierten Semester die Elektrodynamik auf dem Plan. Zunächst werden stationäre (also zeitlich konstante) elektrische Felder behandelt. Darauf folgen stationäre Magnetfelder. Schließlich werden zeitlich veränderliche elektromagnetische Felder behandelt. Damit die ganze Rechnung etwas schöner und etwas einfacher wird, wird die spezielle Relativitätstheorie eingeführt und die ganze Berechnung relativistisch durchgeführt. Mit so netten Spielereien wie der Lorentztransformation, die dem Zugreisenden sagt, was er sieht, wenn er die Welt außerhalb des Zuges betrachtet, kann man durchaus Stunden verbringen. Aber Relativitätstheorie ist nicht nur die Theorie von Reisenden in Zügen, die ihre Uhren vergleichen und Lichtsignale versenden, und von Zwillingen in Raumschiffen, die jünger geblieben sind als ihre Zwillinge auf der Erde. Auch elektromagnetische Felder kann man transformieren - und damit z.B. herleiten, warum eine beschleunigte Ladung Strahlung aussendet. Dass sie das tut, kann man an der Stromrechnung des DESY ablesen: Die Teilchen, die auf einer Kreisbahn gehalten werden, geben sehr viel Energie in Form von Strahlung ab. Diese muss ständig nachgeführt werden. Aber man nutzt diese Synchrotronstrahlung auch aus: Als Quelle für intensive Röntgenstrahlung dient der Beschleuniger DORIS am HASYLAB (dort arbeitet mein Chef): Materialforschung wird dort ebenso betrieben wie medizinische Forschung.
Richtig interessant wird aber erst die allgemeine Relativitätstheorie. Die entsprechende Vorlesung besuche ich bereits. Es ist wirklich faszinierend zu sehen, wie aus ein paar Annahmen und einigen geometrischen Überlegungen die Einsteinschen Feldgleichungen hervorgehen. Diese bilden die Grundlage der ART: Die Materie sagt dem Raum, wie er sich krümmen soll, und der Raum sagt der Materie, wie sie sich bewegen soll. Wenn man die Gleichungen hat, kann man nach speziellen Lösungen suchen. Eine bekannte Lösung stammt von Karl Schwarzschild, der den Raum um einen Stern betrachtete. Diese Lösung gilt auch für schwarze Löcher. Die Betrachtung eines solchen schwarzen Loches liefert faszinierende Einsichten: Warum ist es schwarz? Warum kann keine Information nach außen gelangen? Was passiert beim Sturz ins schwarze Loch? Antworten bekommt man aber nur, wenn man ein brauchbares Koordinatensystem wählt, in dem man die Gleichungen auch lösen kann. Das ist meistens die eigentliche Schwierigkeit...
Leider passen ART und Quantentheorie nicht gut zusammen. Doch es gibt Ansätze: Einer davon ist die Stringtheorie. Der bekannte Stringtheoretiker Jan Louis hält zur Zeit eine Vorlesung zu diesem Thema. Die Gleichungen sind lang und abstrakt, lieferen aber brauchbare Ergebnisse. Eines davon besagt z.B., dass das Universum eigentlich nicht vier Dimensionen (drei räumliche und eine zeitliche), sondern zehn besitzt. Darin existieren die Teilchen nicht als Punktteilchen, sondern als winzige schwingende Saiten, eben als Strings. Das schöne dabei ist, dass die Gravitation auch mitspielt: als eine von vier Kräften, die doch eigentlich nur verschiedene Ausprägungen einer einzigen vereinheitlichten Kraft sind.
Für den Impuls (die Fachbereichszeitschrift) habe ich einen Artikel über Jan Louis geschrieben, der Ende dieses Semesters veröffentlicht wird. Dann maile ich einen Link auf die Impuls-Seite.
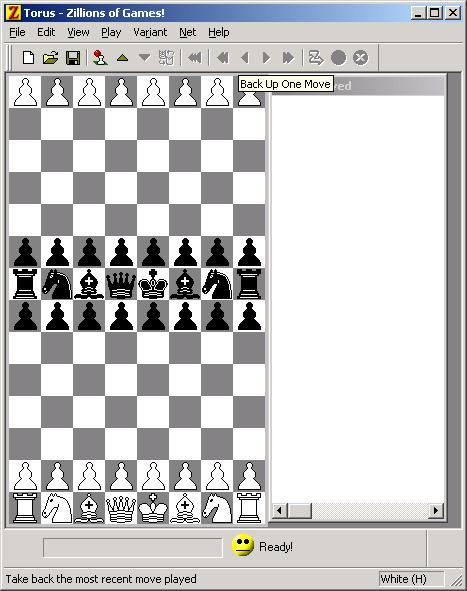
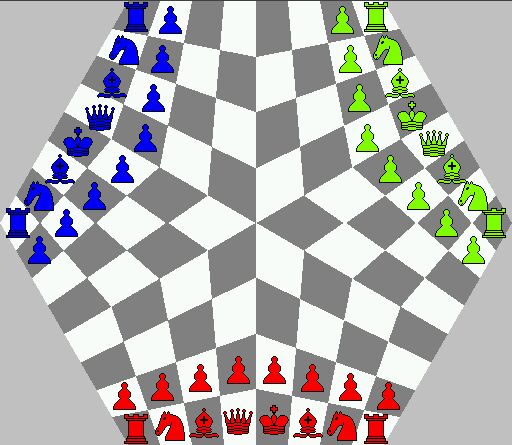
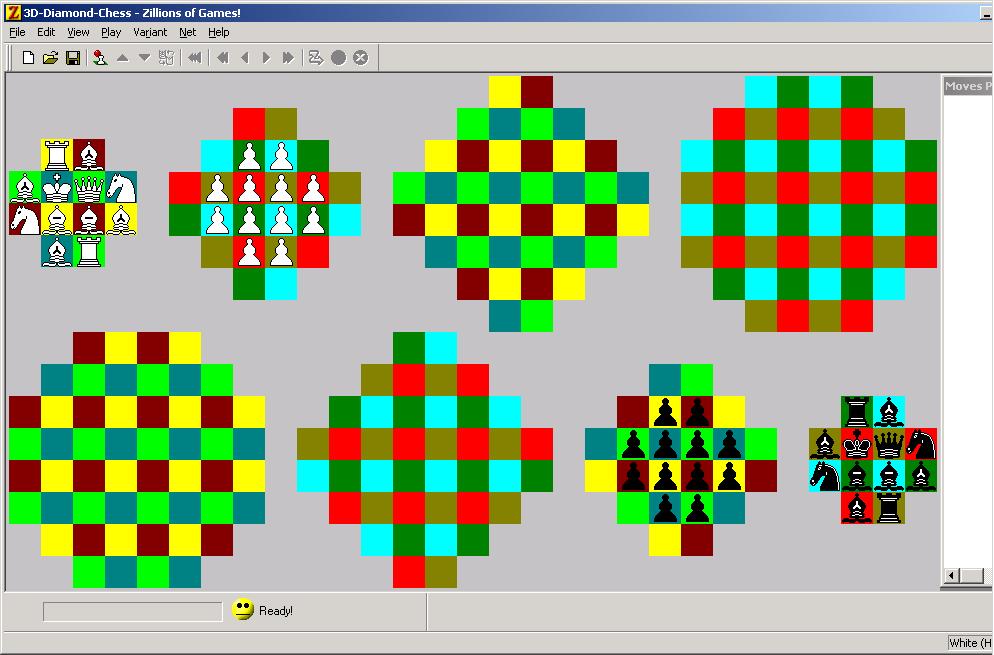
In den Pfingstferien habe ich schließlich noch Gelegenheit gefunden, an meiner Schachtheorie weiterzuarbeiten. Unter anderem habe ich eine neue Darstellungsmöglichkeit für ein Schachbrett gefunden: Ein solches Objekt bezeichne ich als "Funktioid", weil es eine Verallgemeinerung einer Funktion (also einer Abbildung) darstellt. Tatsächlich ist ein Schachbrett nichts weiter als ein besonderes Funktioid. Dabei taucht in meiner Theorie jetzt auch die Symmetriegruppe des n-dimensionalen Würfels auf. Das ist die Menge aller Abbildungen, die einen Würfel (ein Quadrat, einen Hyperwürfel...) in sich selbst überführt. Das hängt damit zusammen, dass Felder eine Würfelform haben sollen, um sie sinnvoll zusammensetzen zu können. Aber dazu habe ich noch nichts geschrieben, ich habe diese Entdeckung erst gestern gemacht, nachdem ich mir mit einem Buch über algebraische Topologie (keine Erklärung, was das ist!) einen geistigen Knoten in den Kopf gelesen habe. Dabei habe ich eine ganze Menge neuer Schachvarianten gefunden und programmiert. Anbei sind ein paar Bilder davon. Das ganze habe ich mit Zillions of Games programmiert. Das ist ein Programm, das praktisch jedes Brettspiel spielen kann. Man kann unter http://www.zillions-of-games.com eine Demoversion herunterladen. Nach der Freischaltung (25$) kann man eigene Spiele programmieren oder kostenlos herunterladen. So habe ich z.B. Schach auf einen Möbiusband programmiert.
Hier gibt es meine Schachvarianten für Zillions of Games zum Download.